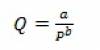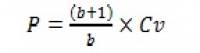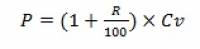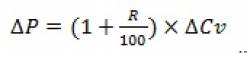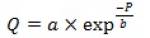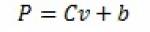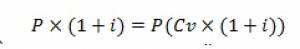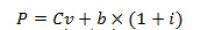Мой друг Василий Самокатов

Определение функциональной зависимости спроса от цены

Зачастую предлагается моделировать зависимость спроса от цены линейной функцией. Однако ясно, что это чрезвычайно упрощенная модель. Все экспериментальные данные дают для спроса зависимость, очень сильно отличающуюся от линейной.

Рассмотрим два варианта функции спроса, которые в какой-то степени отвечают экспериментальным результатам – гиперболу и падающую экспоненту.

Пусть спрос представляет собой гиперболу, описываемую уравнением

(13)

,где

Q –спрос,

P-цена,

a и b – константы, характеризующие спрос на конкретный товар.

Подставив функцию (13) в условие (12), получим выражение для оптимальной цены

(14)

Поскольку константа больше 1 (иначе спрос рос бы с увеличением цены), выражение может быть записано в виде

(15)

где R – рентабельность продажи.

Таким образом, гиперболический вид зависимости спроса от цены делает оптимальным ценообразование по методу прямых затрат, а метод прямых затрат, в свою очередь неявно предполагает гиперболический вид зависимости спроса от цены.

Рассмотрим теперь, как принятый характер функции спроса влияет на принимаемые решения.

Пусть продавец путем проб и ошибок нашел оптимальную с точки зрения прибыли цену. Допустим, поставщик поднял цену на товар, в результате чего закупочная цена у торговца (представляющая собой переменные затраты), увеличилась на . В случае, если функция спроса – гипербола, оптимальным поведением для продавца будет увеличение цены продажи на

(16)

т.е. накрутка на прирост закупочной цены своего обычного процента. При этом торговец автоматически получит цену, оптимальную с точки зрения прибыли.

Рассмотрим, как должна меняться оптимальная цена из-за инфляции. Инфляция предполагает, что со временем все цены (и закупочная и цена продажи) увеличиваются в одинаковой пропорции. Если одновременно в равное число раз увеличатся цена продажи и переменные издержки, то отношение между ними не изменится. Следовательно, не изменится и отношение

, а как результат – постоянным остается коэффициент b. Таким образом, функция спроса, описанная гиперболой, в результате инфляции изменяется так, что оптимальная цена определяется исключительно переменными затратами и установленной рентабельностью.

Проведем аналогичный анализ падающей экспоненты – функции спроса вида

(17)

Подстановка функции (17) в условие максимальной прибыли (12) дает для оптимальной цены выражение

(18)

Оптимальное поведение продавца при этом существенно отличается от случая гиперболической зависимости спроса от цены. Если изначально продажа велась по оптимальной цене, то при повышении закупочной цены на некоторую величину следует на ту же величину (без накрутки рентабельности) поднять цену продажи.

Определим, как должны меняться константы в функции спроса в связи с инфляцией . Условие инфляции (увеличение со временем закупочных цен и цены продажи в одинаковой пропорции можно записать) как

(19)

Подстановка этого условия в выражение (18) дает соотношение

(20)

,где i – коэффициент инфляции.

Можно утверждать, что, при экспоненциальной функции спроса, в случае если закупочная цена остается постоянной, оптимальная цена продажи со временем, тем не менее, растет.

Полученные результаты для разного характера зависимости спроса от цены следует сравнить с реальным изменением цены в зависимости от времени и от затрат.