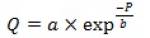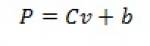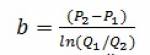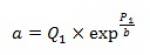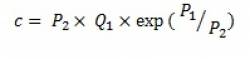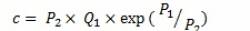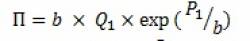Мой друг Василий Самокатов

Сопоставление с реальным изменением цен

для каждого типа каждой функциональной зависимости спроса от цены характерным является свое, не похожее на другие, поведение продавцов.

Можно предположить, что продавцы стремятся достичь наибольшей прибыли и среднеотраслевые цены устанавливаются на уровне, близком к оптимальным. В таком случае наблюдение за среднеотраслевыми ценами дает возможность сделать заключение о функциональном характере зависимости спроса от цены.

Наиболее подходящими для наблюдения являются события, когда на рынке происходили очень значительные изменения уровня цен – при этом малыми сдвигами потребительских предпочтений можно пренебречь. Ценовые сдвиги нужной интенсивности наблюдались в России в 90-х годах прошлого века.

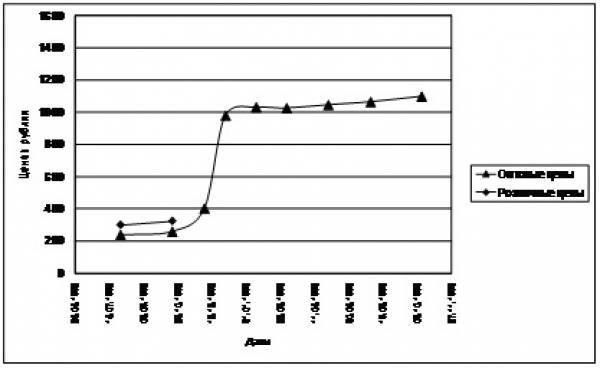
На рисунке (Рис. 32) показано изменение оптовой цены десятка яиц[1]. Характерной особенностью рынка сельхозпродукции на тот момент была сильная зависимость оптовых цен от времени года. Зерно нового урожая в условиях высокой инфляции оказывалось в разы дороже зерна прошлого урожая. Соответственно, себестоимость животноводческой продукции (и оптовая цена, подсчитываемая именно как себестоимость с процентной накруткой) увеличивалась в такой же пропорции каждую осень.

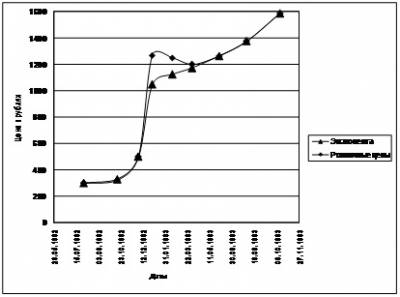
На рис. показан уровень средних розничных цен до момента такого скачка.

Рис. 32 Оптовая цена десятка яиц.

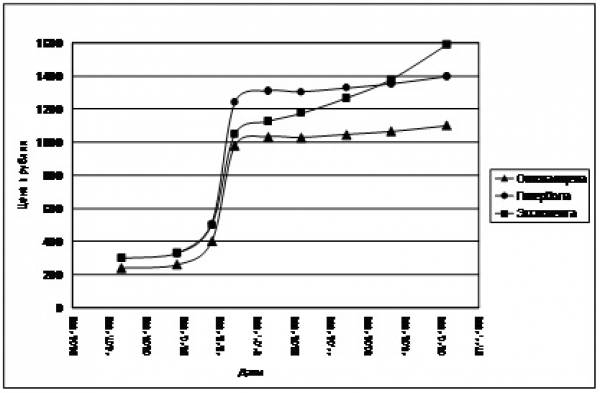
Соотношение оптовых и розничных цен позволяет спрогнозировать изменение розничных цен для различных вариантов функции спроса (Рис. 33). Линейная и квадратичная зависимости при столь значительном изменении оптовой цены дают абсурдный результат – оптимальная цена продажи оказывается меньше цены закупки. Для того, чтобы оценить гиперболическую и экспоненциальную зависимости сравним их с реальным изменением цен в тот же период.

Рис. 33 Прогноз цены на основе различных типов функции спроса.

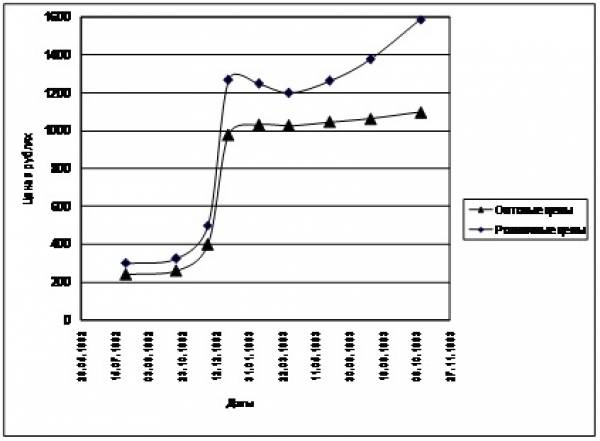
На рисунке (Рис. 34) показано изменение средней розничной цены десятка яиц за тот же период времени[2].

Рис. 34 Средняя стоимость десятка яиц в оптовой и розничной торговле.

На следующих рисунках статистика стоимости десятка яиц в розничной продаже моделируется математическими функциями различных типов.

Рис. 35. Сравнение фактической средней цены с полученной в предположении гиперболической зависимости спроса от цены.

Из рисунка (Рис. 35) видно, что в случае использования гиперболы (функции вида 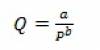) на начальном этапе теоретические значения оптимальной цены полностью совпадает с фактической среднерыночной ценой (следует отметить, что оптимальная цена для гиперболы предполагает сохранение постоянного процента прибыли к прямым затратам, см выражение (16)). Однако затем на розничном рынке наблюдается снижение цены, из чего можно сделать вывод, что произошло затоваривание, и, полученная таким образом цена, не является оптимальной. В течении всего последующего года наблюдалось значительное расхождение теоретической и среднерыночной цены.

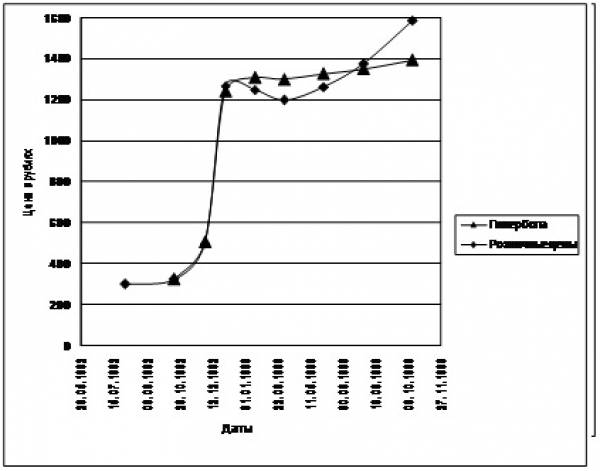
Если же рассматривать в качестве функции спроса падающую экспоненту (Рис. 36), то совпадение прогнозируемой и среднерыночной цены, для большинства временных моментов, удивительно точное. Существенное отличие оптимальной цены, подсчитанной с помощью этой функции, от среднерыночной наблюдалось только в момент резкого изменения оптовой цены, пока розничная цена еще не устоялась. Очень хорошее совпадение результатов использования этой функции с фактами наблюдалось для целого ряда других товаров.

Так, события «черного вторника», когда произошло резкое изменение валютного курса, вызвали сильные колебания розничной цены на бытовую электронику, которая, тем не менее, в итоге сформировалась на уровне, предсказанном исходя из экспоненциальной зависимости спроса от цены.

Таким образом, можно считать, что определен характер зависимости спроса от цены, а именно функция вида

.

Зная эту зависимости можно строить ценовую политику оптимальным образом.

Так, если продажи одного товара по цене P1 составили Q1, а по отличающейся от него цене P2 – Q2, то наибольшую прибыль обеспечит цена

(21)

где

Cv – переменные затраты;

b– оптимальная наценка, которая может быть определена как

(22)

Объем продаж при этой цене будет определятся выражением (17), в котором коэффициент a может быть определён как

(23)

Рис. 36 Сравнение фактической средней цены с полученной в предположении экспоненциальной зависимости спроса от цены.

Исходя из экспоненциального характера зависимости спроса от цены может быть определена выручка при переходе от цены P1 к цене P2:

(24)

Так, выручка при цене, обеспечивающей наибольшую прибыль составляет

(25)

, а величина прибыли –

(26)

Безусловно, гипотеза об экспоненциальном характере функции спроса требует дальнейшей проверки.